How to Morph Planar Graph Drawings
Face up morphing has become quite popular in the final years; from mixing the faces of two celebrities to guessing how your babe could look, many TV shows and apps utilise software which changes one face into another through a continuous and smooth transition.

Amongst the unlike mathematical tools that can be used for face morphing, one of the easiest to understand is the morphing of triangulations. In this arroyo, a number of critical points are selected (eastward.g., the highest signal of the nose, or the leftmost and rightmost points of the oral cavity) and a triangulation of those points is considered.

Back in 1944, Cairns one proved that such a pair of triangulations, topologically equivalent, can be morphed one into the other while preserving planarity (i.eastward., avoiding segment crossings at the intermediate steps). The proof was by consecration, based on contracting a vertex of low degree to a neighbor, and needed an exponential number of steps. Information technology took nearly 40 years until, in 1983, Thomassen 2 extended the proof to all planar straight-line drawings, not necessarily triangulations. Nevertheless, the idea of this proof was augmenting those input drawings to isomorphic triangulations, and then using Cairns' result.


Later in 1999, Floater and Gotsman iii provided an alternative method for morphing triangulations based on Tutte's graph cartoon algorithm 4, further extended to all planar direct-line drawings past Surazhsky and Gotsman 5. A drawback of these algorithms is that they do not provide explicit trajectories for the vertices, calculating instead a snapshot at the requested time points.
Finding vertex trajectories is precisely the achievement of a contempo piece of work on how to morph planar graph drawings, by Alamdari et al. vi, where each stride is a unidirectional linear morph, i.e., every vertex moves at abiding speed forth a straight line (although the speeds of the vertices may differ). The authors succeed in obtaining an algorithm which uses only a linear number of steps, beating the exponential number in Cairns' seminal paper, and they further testify that this complexity is worst-case optimal.
For an overview of the techniques, as in a higher place, the approach in the paper has 2 parts. First, solving the problem for the special case of triangulations, and and so reducing the general problem for all planar directly-line drawings to that particular instance of triangulations. For the case of triangulations, the thought is like to the approach by Cairns: Finding a vertex ![]() that, in both triangulations, can be contracted to a neighbour
that, in both triangulations, can be contracted to a neighbour ![]() while preserving planarity. This contraction provides two planar drawings of a smaller graph, for which recursion is used.
while preserving planarity. This contraction provides two planar drawings of a smaller graph, for which recursion is used.
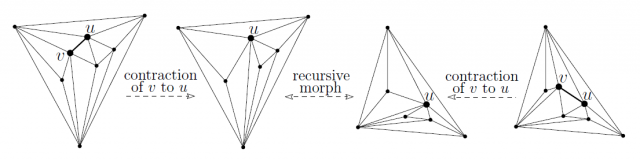
Such a programme has a couple of issues, the first 1 being that there might not be a vertex ![]() as above. The authors overcome this by choosing an interior vertex
as above. The authors overcome this by choosing an interior vertex ![]() of caste at most five (which exists because of the graph being planar) and morphing the commencement drawing so that the neighbors of
of caste at most five (which exists because of the graph being planar) and morphing the commencement drawing so that the neighbors of ![]() form a polygon such that one of them, chosen as
form a polygon such that one of them, chosen as ![]() , is able to "run into" the whole polygon. Again, this mimics Cairns' arroyo, but the authors manage to cut downwards his exponential number of steps to merely two. The second issue is that the contraction should not brand a vertex become coincident with another, just making them be shut enough. Since Cairns' solution resulted in a nonlinear motion, here the authors piece of work out a dissimilar way of finding suitable positions.
, is able to "run into" the whole polygon. Again, this mimics Cairns' arroyo, but the authors manage to cut downwards his exponential number of steps to merely two. The second issue is that the contraction should not brand a vertex become coincident with another, just making them be shut enough. Since Cairns' solution resulted in a nonlinear motion, here the authors piece of work out a dissimilar way of finding suitable positions.
For a bit of further detail, the core of the algorithm is a solution to the quadrilateral convexification trouble: given a triangulation which contains a nonconvex quadrilateral, find a morph which makes that quadrilateral convex.
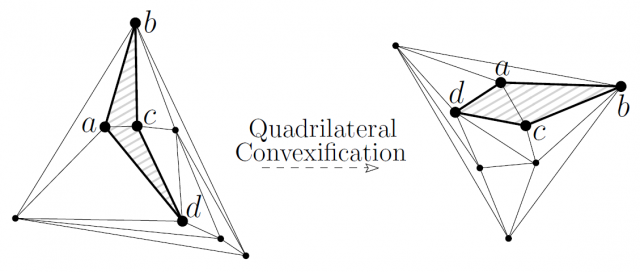
In order to exercise so, permit ![]() exist the vertices of the quadrilateral and we assume, without loss of generality, that
exist the vertices of the quadrilateral and we assume, without loss of generality, that ![]() is the reflex vertex of the nonconvex quadrilateral, i.due east., the one with interior angle larger than 180 degrees. This implies that
is the reflex vertex of the nonconvex quadrilateral, i.due east., the one with interior angle larger than 180 degrees. This implies that ![]() is the tip of the arrowhead shape of the quadrilateral and that the triangulation contains the edge
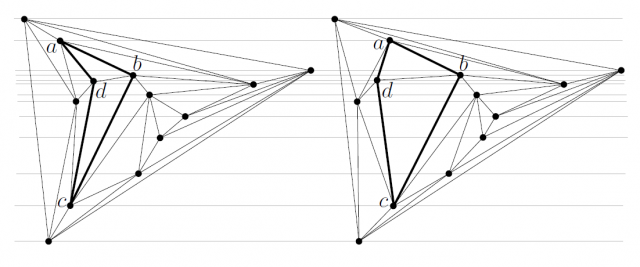
is the tip of the arrowhead shape of the quadrilateral and that the triangulation contains the edge ![]() (see the previous figure). So, the authors change the frame of reference so that this edge
(see the previous figure). So, the authors change the frame of reference so that this edge ![]() is almost horizontal, then that they can use a issue, by Hong and Nagamochi 7, which allows to redraw a plane graph, with only horizontal movements of the vertices, to attain convex faces.
is almost horizontal, then that they can use a issue, by Hong and Nagamochi 7, which allows to redraw a plane graph, with only horizontal movements of the vertices, to attain convex faces.
This paper by Alamdari et al., which collects the efforts of thirteen authors past combining four different conference papers, is a remarkable example of how collaboration can boost scientific discipline further than competition to solve a trouble with more one century of history viii.
Notation: This text is part of the dissemination activities of the Marie Skłodowska-Curie grant No 734922 in the European Union's Horizon 2020 research and innovation programme.
southernpothead1969.blogspot.com
Source: https://mappingignorance.org/2018/02/21/triangulations-face-morphing/
Post a Comment for "How to Morph Planar Graph Drawings"